Penerapan fungsi dalam ekonomi dan bisnis merupakan salah satu bagian yang sangat penting untuk dipelajari, karena model-model ekonomi yang berbentuk matematika biasanya dinyatakan dengan fungsi. Fungsi dalam matematika menyatakan suatu hubungan formal di antara dua himpunan data. Jika himpunan data tersebut adalah variabel, maka fungsi dapat dikatakan sebagai hubungan antara dua variabel.
Fungsi adalah Suatu bentuk matematis yang menyata kan hubungan ketergantungan (hubungan fungsional) antara satu variabel dengan variabel lainnya. Unsur-unsur pembentuk fungsi adalah variabel, koefisien, dan konstanta.
- Variabel adalah unsur yang sifatnya berubah-ubah dari satu keadaan ke keadaan lainnya. Variabel dapat dibedakan menjadi variabel bebas dan variabel terikat. Variabel bebas : variabel yang menjelaskan variabel lainnya. Adapun Variabel terikat adalah variabel yang diterangkan oleh variabel bebas.
- Koefisien adalah bilangan atau angka yang diletakkan tepat di depan suatu variabel, terkait dengan variabel yang bersangkutan.
- Konstanta sifatnya tetap dan tidak terkait dengan suatu variabel apapun.
Contoh: Y = 0,8X + 5
Keterangan:
- X = Variabel bebas (Independent variabel) adalah variabel yang nilainya tidak tergantung pada variabel lain.
- Y = Variabel terikat (Dependent variabel) adalah variabel yang nilainya tergantung pada variabel lain.
- 0,8 = adalah koefisien variabel X
- 5 = adalah konstanta
A. Pengertian Fungsi Linier
Fungsi Linier adalah fungsi Polinom yang variabel bebasnya memiliki pangkat paling tinggi adalah satu. Dikatakan fungsi linier apabila variabel X dan Y dalam persamaan tersebut mempunya pangkat satu (sehingga X1=X dan Y1=Y). Oleh karena itu fungsi linier sering disebut dengan persamaan garis lurus (pgl) dengan bentuk umumnya adalah sebagai barikut:
Bentuk umum fungsi linier 2 variabel (x & y)
y = a0 + a1x
Dimana :
a0 konstanta, nilainya positif, negatif, atau nol
a1 koefisien, nilainya positif, negatif, atau nol
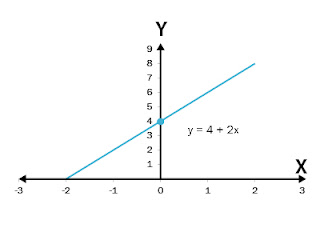
Contoh : y = 4 + 2x
Bentuk umum fungsi linier 2 variabel (x & y)
y = a0 + a1x
Dimana :
a0 konstanta, nilainya positif, negatif, atau nol
a1 koefisien, nilainya positif, negatif, atau nol
Contoh : y = 4 + 2x
f : x → mx + c atau f(x) = mx + c atau y = mx + c
- m adalah gradien / kemiringan / kecondongan (2)
- c adalah konstanta (4)
Contoh lain fungsi linier:
y=2x+5
y=-3x+2
Didalam menyelesaikan persoalan fungsi linier ada dua cara yang perlu diketahui, yaitu:
1. Membuat kurva fungsi linier
Adapaun cara membuat kurva liner antaralain:
a. Dengan cara sederhana (curve traicing process)
Yaitu dengan menggunakan tabel x dan y, dimana kita tentukan dulu nilai x sebagai variabel bebas, maka dengan memasukkan beberapa nilai x kita akan memperoleh nilai y.
Misalkan : y = 4 + 2x
| x | -2 | -1 | 0 | 1 | 2 |
| y | 0 | 2 | 4 | 6 | 8 |
Lalu titik-titik dalam tabel tersebut ditandai dan dihubungkan menghasilkan garis seperti dalam kurva berikut ini:
Yaitu dengan mencari titik potong untuk sumbu x dan juga sumbu y.
Langkah-langkah membuat grafik fungsi linier dengan cara matematis:
- Tentukan titik potong dengan sumbu x, y = 0 diperoleh koordinat A( x1, 0)
- Tentukan titik potong dengan sumbu y, x = 0 diperoleh koordinat B( 0, y1)
- hubungkan dua titik A dan B sehingga terbentuk garis lurus.
contoh:
Misalkan diketahui y = 4 + 2x. Maka grafik fungsi dapat digambarkan menggunakan ciri-ciri penting, yaitu:
- Titik potong fungsi dengan sumbu y, x=0, maka y=4. Jadi titiknya adalah A(0,4)
- Titik potong fungsi dengan sumbu x, y=0, maka x=-2. Jadi titiknya adalah B(-2,0)
Dengan menggunakan kedua ciri ini maka kita dapat menggambar grafik fungsi y=4 + 2x seperti terlihat pada gambar berikut:
2. Bentuk Kurva Suatu Fungsi
Persamaan linier juga dapat ditulis ditulis dengan simbol y = ax + b (ini untuk mempermudah dalam memahami gambar)
- Jika b bernilai positif : fungsi linier digambarkan garis dari kiri bawah ke kanan atas
- Jika b bernilai negatif : fungsi linier digambarkan garis dari kiri atas ke kanan bawah
- Jika b bernilai nol : digambarkan garis yg sejajar dengan sumbu datar x
- Apabila b bernilai negatif, contoh: Y = 10 - 2X maka kurva bergerak dari kiri atas ke kanan bawah seperti gambar berikut:
- Apabila b bernilai positif, misalnya : Y = 3 + 2X maka kurva bergerak dari kiri bawah ke kanan atas seperti gambar berikut:
3). Gradien dan Persamaan garis lurus
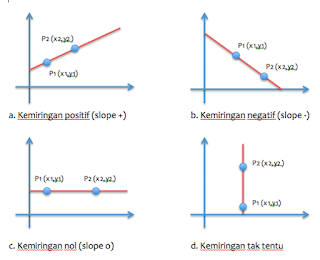
Gradien adalah koefisien yang menentukan arah garis fungsi linier, biasanya koefisien ini melekat pada variabel X (sisi vertikal)/(sisi horizontal).
Jika gambar kurva bergerak dari kiri atas ke kanan bawah maka nilai gradiennya negatif dan juga sebaliknya.
Contoh:
y=-x+3
Jika x=0 → y=3, koordinat (0,3)
Jika y=0 → x=3, koordinat (3,0)
a. Garis lurus yang melalui titik A(x1, y1) dan B(x2, y2) memiliki gradien m:
m = y1-y2 / x1-x2 atau m = y2-y1/x2-x1
b. Persamaan garis lurus yang melalui titik A(x1, y1) dan B(x2, y2) adalah:
- y-y1 = x-x1
- y2-y1=x2-x1
c. Persamaan garis lurus yang bergradien m dan melalui titik A(x1, y1), fungsinya adalah:
y = m (x – x1 ) + y1
4. Hubungan dua garis lurus
- Dua garis lurus yang sejajar
Sejajar kan terjadi ketika dua buah garis akan sejajar apabila kemiringan garis yang satu sama dengan kemiringan garis yang lain (m1 = m2).
- Dua garis lurus yang berhimpit
Berimpit akan terjadi ketika dua buah garis akan berimpit apabila persamaan garis yang satu merupakan kelipatan dari (proporsional terhadap) persamaan garis yang lain. y1 = mx1+ b1 akan berimpit dengan y2 = mx2+ b2 , jika y1 = ny2 ; a1 = na2 ; b1 = nb2.
- Dua garis lurus yang berpotongan
Berpotongan, dua buah garis akan berpotongan apabila kemiringan garis yang satu tidak sama dengan kemiringan garis yang lain (m1 ≠ m2).
Untuk fungsi linier yang saling berpotongan, maka untuk mencari titik potongnya dapat dilakukan dengan cara :
Untuk fungsi linier yang saling berpotongan, maka untuk mencari titik potongnya dapat dilakukan dengan cara :
- Metode Grafik
- Metode Subtitusi
- Metode Eliminasi
- Metode Campuran
- Dua garis lurus yang tegak lurus
Tegak lurus (termasuk garis lurus berpotongan) akan terjadi saat dua garis akan saling tegak lurus apabila kemiringan garis yang satu merupakan kebalikan dari kemiringan garis yang lain dengan tanda yang berlawanan (m1 = – 1/m2). Atau nilai perkalian kemiringannya menghasilkan nilai –1 (m1 ⨉ m2 = -1).
B. Penggunaan Fungsi Linear dalam Ekonomi
Penerapan suatu fungsi dalam ekonomi sangatlah banyak entah itu fungsi linier maupun non-linier. Fungsi linier sering dijumpai dalam suatu analisa yang membutuhkan suatu kurva. Oleh karena itu materi fungsi khususnya fungsi linier wajib untuk dikuasai. Berikut ini adalah beberapa contoh penerapan fungsi linier di bidang ekonomi:
1. Penerapan Fungsi Linier Pada Fungsi Permintaan (Demand Function)
Fungsi Permintaan menunjukkan hubungan antara harga dengan jumlah barang yang diminta oleh konsumen dengan anggapan bahwa faktor-faktor lain tetap (ceteris paribus), yaitu selera tetap, pendapatan tetap dan harga barang-barang lain tetap, maka ini menandakan bahwa apabila harga turun jumlah barang yang diminta oleh konsumen naik, demikian pula sebaliknya.
Penerapan suatu fungsi dalam ekonomi sangatlah banyak entah itu fungsi linier maupun non-linier. Fungsi linier sering dijumpai dalam suatu analisa yang membutuhkan suatu kurva. Oleh karena itu materi fungsi khususnya fungsi linier wajib untuk dikuasai. Berikut ini adalah beberapa contoh penerapan fungsi linier di bidang ekonomi:
1. Penerapan Fungsi Linier Pada Fungsi Permintaan (Demand Function)
Fungsi Permintaan menunjukkan hubungan antara harga dengan jumlah barang yang diminta oleh konsumen dengan anggapan bahwa faktor-faktor lain tetap (ceteris paribus), yaitu selera tetap, pendapatan tetap dan harga barang-barang lain tetap, maka ini menandakan bahwa apabila harga turun jumlah barang yang diminta oleh konsumen naik, demikian pula sebaliknya.
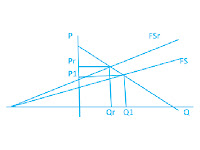
1. Pada saat harga turun P1 ke P2, maka permintaan naik dari Q1 ke Q2
2. Pada saat harga naik P1 ke P3, maka per mintaan turun dari Q1 ke Q3
Hal –hal yang perlu diperhatikan:
1. P = harga per unit; Q = Quantitas barang
2. Kurva permintaan bergerak dari kiri atas ke kanan bawah
3. P dan Q positif
4. Pada suatu tingkatan harga (P) hanya terkandung nilai kuantitas (Q) dan sebaliknya
5. Skala P dan Q tidak perlu sama, karena harga tidak sama dengan kuantitas.
2. Penerapan Fungsi Linier Pada Fungsi Penawaran (Supply Function)
Fungsi Penawaran menunjukkan hubungan antara harga dengan jumlah barang yang ditawarkan kepada konsumen, dengan anggapan faktor-faktor lain tetap (ceteris paribus). Maka apabila tingkat harga meningkat, jumlah barang yang ditawarkan bertambah, demikian pula sebaliknya.
1. Pa → Pc : Jumlah barang yang ditawarkan naik Qa → Qc
2. Pa → Pb : Jumlah barang yang ditawarkan turun Qa → Qb
3. Penerapan Fungsi Linier Pada Market Equilibrium (Keseimbangan Pasar)
Pasar suatu jenis barang dikatakan berada dalam keseimbangan apabila jumlah barang yang diminta dipasar tersebut sama dengan jumlah barang yang ditawarkan. Secara matematik dan grafik hal ini ditunjukkan oleh persamaan :
FS = FD
( Fungsi Penawaran = Fungsi Permintaan)
Yaitu pada perpotongan kurva permintaan dengan kurva penawaran. Pada posisi keseimbangan pasar ini tercipta harga keseimbangan (equilibrium price) dan Jumlah keseimbangan (equilibrium quantity).
4. Penerapan Fungsi Linier Pada Pajak
Pajak adalah jenis pungutan yang dilakukan pemerintah terhadap produsen/penjual sehingga beban pajak akan menambah besarnya biaya yang harus dipikul oleh produsen/penjual. Akibatnya harga yang ditawarkan akan naik, kenaikannya sebesar pajak yang dibebankan. Ada dua macam pajak, antara lain:
a. Pajak Perunit
Pajak per unit adalah pajak yang dikenakan terhadap suatu barang yang besarnya tetap untuk setiap unit barang.
Fungsi sebelum pajak : FS → P = aQ + b
Fungsi setelah pajak : FSt → P = (aQ + b) + t
- Pajak yang ditanggung konsumen: (Pt – P) Qt
- Pajak yang ditanggung produsen: (Qt .t)- (Pt – P) Qt
- Pajak yang diterima pemerintah: Qt.t
b. Pajak Persentase
Pajak Persentase adalah pajak yang dipungut pemerintah dengan persentase yang tetap terhadap penjualan. Pajak persentase (r).
Fungsi sebelum pajak : FS → P = aQ + b
Setelah Pajak : FSr→P = (aQ + b)( 1 + r )
5. Penerapan Fungsi Linier pada Subsidi
Subsidi merupakan kebalikan dari pajak, pengaruhnya terhadap keseimbangan pasar berbalikan dengan pengaruh pajak. Subsidi yang diberikan atas produksi/penjualan suatu barang menyebabkan harga jual barang tersebut menjadi rendah. Dengan adanya subsidi, produsen merasa ongkos produksinya menjadi lebih kecil sehingga bersedia menjual lebih murah.
Fungsi sebelum subsidi : FS → P = aQ + b
Fungsi setelah subsidi : FSs → P = aQ + b – S












Terimakasih suhu
ReplyDelete